Page 1 :
PHOENIX INSTITUTE OF MATHEMATICS, State Council Of Educational Research and Training, Maharashtra, Pune, QUESTION BANK, STD XII Arts and Science Stream, MATHEMATICS AND STATISTICS (40), Part-I, 1. MATHEMATICAL LOGIC, , Q1) Select and write the most appropriate answer from the given, alternatives:, i), , ii), , iii), , iv), , v), , Which of the following statement is true, a) 3 + 7 =4 or 3 – 7 = 4, b) If Pune is in Maharashtra, then Hyderabad is in Kerala, c) It is false that 12 is not divisible by 3, d) The square of any odd integer is even., Which of the following is not a statement, a) 2+2 =4, b) 2 is the only even prime number, c) Come here, d) Mumbai is not in Maharashtra, If p is any statement then ( p ˅ ̴ p) is a, a) Contingency, b) Contradiction, c) Tautology, d) None of these, If p and q are two statements , then ( p → q ) ↔ ( ̴ q → ̴ p) is, a) Contradiction, b) Tautology, c) Neither (i) nor (ii), d) None of these, Negation of p → ( p˅ ̴ q) is, a) ̴ p → ( ̴ p ˅ q), b) p ˄ ( ̴ p ˄ q ), c) ̴ p ˅ ( ̴ p ˅ ̴ q), d) ̴ p → ( ̴ p → q ), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 2 :
PHOENIX INSTITUTE OF MATHEMATICS, vi), , If p : He is intelligent, q : He is strong, Then, symbolic form of statement “It is wrong that, he is intelligent, or strong “ is, a) ̴ p ˅ ̴ q, b) ̴ ( p ˄ q), c) ̴ ( p ˅ q), d) p ˅ ̴ q, vii) A biconditional statement is the conjunction of two --------------statements, a) Negative, b) Compound, c) Connective, d) Conditional, viii) If p → q is an implication , then the implication ̴ q → ̴ p is called, its, a) Converse, b) Contrapositive, c) Inverse, d) Alternative, The negation of the statement (p ˄ q) → ( r ˅ ̴ p), a) p ˄ q˄ ~ r, b) ( p ˄ q) ˅ r, c) p ˅ q ˅ ~ r, d) ( p v q) ˄ ( r ˅ s), x) The false statement in the following is, a) p ˄ ( ̴ p) is contradiction, b) ( p → q ) ↔ ( ̴ q → ̴ p ) is a contradiction, c) ̴ ( ̴ p ) ↔ p is a tautology, d) p ˅ ( ̴ p ) ↔ p is a tautology, Q 2 ) Attempt the following, 1 marks, ix), , i) Find the negation of 10 + 20 = 30, ii) State the truth Value of x2 = 25, iii) Write the negation of p → q, iv) State the truth value of √3 is not an irrational number, v) State the truth value of (p ˅ ̴ p), vi) State the truth value of (p ˄ ̴ p), UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 3 :
PHOENIX INSTITUTE OF MATHEMATICS, Q3) Attempt the following, i), , 2 marks, , : If statements p, q are true and r, s are false, determine the truth, values of the following., a) ~ p ∧ (q ∨ ~ r), , ii), , b) (p ∧ ~ r) ∧ (~ q ∨ s), , Write the following compound statements symbolically., , iii), , a), , Nagpur is in Maharashtra and Chennai is in Tamilnadu., , b), , Triangle is equilateral or isosceles., , . Write the converse and contrapositive of the following, statements., “If a function is differentiable then it is continuous”., , iv), , Without using truth table prove that :, ~ (p ∨ q) ∨ (~ p ∧ q) ≡ ~ p, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 ), , Answers, i), ii), , a) F, b) F, ii) a) 𝑝 ∧ q b) 𝑝 ∨ q, converse: If function is continuous then it is differentiable., Contrapositive: If function is not continuous then it is not, differentiable., , Q4) Answer the following questions, i), ii), , Write the negation of the statement “ An angle is a right angle if, and only if it is of measure 900”, Write the following statements in symbolic form, a) Milk is white if and only if the sky is not blue, b) If Kutab – Minar is in Delhi then Taj- Mahal is in Agra, c) Even though it is not cloudy , it is still raining, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 4 :
PHOENIX INSTITUTE OF MATHEMATICS, iii), , iv), , Use quantifiers to convert the given open sentence defined on N, into a true statement, a) n2 ≥ 1, b) 3x – 4 < 9, c) Y + 4 > 6, Examine whether the statement pattern is a tautology,, contradiction or contingency, ( p ˄ ̴ q) → ( ̴ p ˄ ̴ q), , v), , Using truth table prove that ̴ p ˄ q ≡ ( p ˅ q ) ˄ ̴ p, , vi), , Write the dual of the following, a) 13 is prime number and India is a democratic country, b ) ( p ˄ ̴ q ) ˅ ( ̴ p ˄ q ) ≡ ( p ˅q ) ˄ ̴ ( p ˄ q), , vii) Write the converse, inverse and contrapositive of the statement, “If it snows, then they do not drive the car”, Q5) Answer the following questions, i), , ii), iii), iv), v), , Examine whether the statement pattern, [p→ ( ̴ q ˅ r)] ↔ ̴ [ p → ( q → r)] is a tautology, contradiction or, contingency., Using truth table prove that p ˅ (q ˄ r) ≡ ( p ˅q) ˄ ( p ˅ r), Without using truth table show that, ( p ˅ q) ˄ ( ̴ p v ̴ q) ≡ ( p v ̴ q ) ˄ ( ̴ p v q ), With proper justification state the negation of, ( p ↔ q) v ( ̴ q → ̴ r ), Prepare truth table for ( p ˄ q) v ̴ r, , 2. MATRICES, I. MCQ (2 marks each ), Q. 1., , 3, The adjoint matrix of [2, 0, , −3 4, −3 4] is, −1 1, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 6 :
PHOENIX INSTITUTE OF MATHEMATICS, 1, Q. 9. The element of second row and third column in the inverse of [ 2, −1, , 2 1, 1 0], 0 1, , is…, a) -2, Q. 10. If A = [, a), , b) -1, , c) 1, , d) 2, , 4 5, ] , then |(2𝐴)−1 | =….., 2 5, , 1, , b), , 30, , 1, , c), , 20, , 1, 60, , d), , 1, 40, , 𝑥−𝑦−𝑧, 0, −𝑦, +, 𝑧, Q. 11. If [, ] =[5] , then the value of x, y and z are respectively…, 𝑧, 3, a) 0, -3, 3, , b) 1, -2 , 3, , c) 5, 2, 2, , d) 11, 8, 3, , Q. 12 The value of x, y, z for the following system of equations, x + y + z = 6, x - y+ 2z = 5, 2x + y -z = 1 are…, a) x = 1, y = 2, z = 3, , b) x = 2, y = 1, z = 3, , c) x = -1, y = 2, z = 3, , d) x = y = z = 3, , 3, Q. 13. If A =[0, 0, a) 33, , 0 0, 3 0] , then |𝐴||𝑎𝑑𝑗𝐴|=…, 0 3, , b) 39, , c) 36, , a) 327, , Q. 14. System of equations x + y = 2 , 2x + 2y = 3 has…., a) no solution, , b) only one solution, , c) many finite solutions., Q. 15., , d) infinite solutions., , 1 −1 1, 4, 2 2, If A = [2 1 −3], 10B = [−5 0 ∝] and B is the inverse of, 1 −2 3, 1 1, 1, , matrix A, then 𝛼 = …., a) -2, , b) -1, , c) 2, , d) 5, , II. Very Short Answers ( 1 mark ), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 7 :
PHOENIX INSTITUTE OF MATHEMATICS, 1 2, Q. 1. If A = [1 1, 2 4, , 3, 5] , then find the value of a31A31+ a32A32+ a33A33, 7, , Q. 2. For an invertible matrix A, if A∙ (adjA) = [, , 10 0, ] ,then find the, 0 10, , value of |𝐴|., 𝛼, Q. 3. If the inverse of the matrix [ 2, 6, , 14 −1, 3, 1 ] does not exists then find the, 2, 3, , value of 𝛼., 2, Q. 4. If A = [, −3, , 2, 0, ] and B = [, 2, 1, , 𝑐𝑜𝑠𝜃, Q. 5. A = [, −𝑠𝑖𝑛𝜃, , −𝑠𝑖𝑛𝜃, ] then find 𝐴−1 ., −𝑐𝑜𝑠𝜃, , 𝑎, Q. 6. If A = [, 𝑐, Q. 7. If A = [, , −1, ] , then find the matrix (𝐵−1 𝐴−1 )−1, 0, , 𝑏, ] then find the value of |𝐴|−1, 𝑑, , 3 1, ], and AB = BA= I , then find the matrix B., 5 2, , 𝑐𝑜𝑠𝛼, Q. 8. If A(𝛼) = [, −𝑠𝑖𝑛𝛼, , 𝑠𝑖𝑛𝛼, ] then prove that 𝐴2 (𝛼) = A(2𝛼), 𝑐𝑜𝑠𝛼, , 1, 2, 1 3 2, Q. 9. If A =[ 3 −2] and B = [, ] then find the order of AB., 4 −1 3, −1 0, 3 −2, Q. 10. A+I = [, ] then find the value of (A+I)(A-I), 4 1, 2 −1 1, Q. 11. If A = [−2 3 −2] then find A2, −4 4 −3, −2 4, Q. 12. If A = [, ] then find A2, −1 2, 𝑥, 0 3 3, Q. 13. If A = [−3 0 −4] and B = [𝑦] , find the matrix 𝐵′ (𝐴𝐵), 𝑧, −3 4 0, III. Short Answers ( 2 marks ), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 8 :
PHOENIX INSTITUTE OF MATHEMATICS, Q. 1. If 𝑓(𝑥) = 𝑥 2 − 2𝑥 − 3 then find 𝑓(𝐴) when A = [, , 1 2, ], 2 1, , −1, Q. 2. If A = [ 2 ] , B = [3 1 −2], find 𝐵′ 𝐴′, 3, Q. 3 If A is invertible matrix of order 3 and |𝐴| = 5, then find |𝑎𝑑𝑗𝐴|, 11 0, 6 5, Q. 4. If A = [, ] and B = [, ] then find 𝐴′ 𝐵′, 0 11, 5 6, 2 4, 1 1, Q. 5. If A = [, ] and B = [, ] then find (𝐴−1 𝐵−1 ), 1 3, 0 1, 2 0, 1, Q. 6. If A = [, ] and B = [ ] then find the matrix 𝑋 such that 𝐴−1 𝑋 = 𝐵, 0 1, 2, 6 17, Q. 7. Find the matrix X such that AX = I where A = [, ], 1 3, Q. 8. Find 𝐴−1 using adjoint method, where A = [, , 𝑐𝑜𝑠𝜃, −𝑠𝑖𝑛𝜃, , 𝑠𝑖𝑛𝜃, ], 𝑐𝑜𝑠𝜃, , Q. 9. Find 𝐴−1 using column transformations :, 5, i) A = [, 3, , 3, ], −2, , ii) A = [, , Q. 10. Find the adjoint of matrix A = [, , 2 −3, ], −1 2, , 6 5, ], 3 4, , 1 2 4, Q. 11. Transform [3 −1 5] into an upper triangular matrix by using suitable row, 2 4 6, transformations., IV. Short answers ( 3 Marks), 0, 4, 3, Q. 1. If A = [ 1 −3 −3], then find A2 and hence find A-1, −1 4, 4, 0 1, 1 2 1, Q. 2 If A =[2 3 ] and B = [, ], then find (AB)-1, 2 1 0, 1 −1, −4 −3 −3, Q. 3. If A = [ 1, 0, 1 ], find adj(A), 4, 4, 3, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 9 :
PHOENIX INSTITUTE OF MATHEMATICS, Q. 4. Solve the following by inversion method 2x + y = 5 , 3x + 5y = - 3, Q. 5. If A=[, , 1 2, 3 −2, , −1, ], apply R1 ↔ R2 and then C1 →C1 + 2C3 on A., 5, , Q. 6. Three chairs and two tables costs ₹ 1850. Five chairs and three tables costs, ₹2850. Find the cost of four chairs and one table by using matrices., 1, 4 5, Q. 7. If A = [, ], show that A-1 = (𝐴 − 5𝐼), 6, 2 1, , 2, Q. 8. Find the adjoint of matrix A =[ 3, −1, , 0 −1, 1 2], 1 2, , 1 2, Q. 9. Find the matrix X such that [2 3, 1 2, , 3, 2, 2 −5, 2] 𝑋 = [−2 −1 4 ] ,, 2, 1, 0 −1, , secθ tanθ 0, Q. 10. Find the inverse of A =[tanθ secθ 0], 0, 0, 1, 1 2 4, Q. 11. Transform [3 −1 5] into an upper triangular matrix by using suitable row, 2 4 6, transformations., 1 0 1, 1 2 3, Q. 12. If A = [0 2 3] and B = [1 1 5] , then find the matrix X such that XA, 1 2 1, 2 4 7, =B, V. Long answers ( 4 Marks), 2 −3 3, Q. 1. Find the inverse of A = [2, 2 3], 3 −2 2, , by using elementary row, , transformations., 1, Q. 2. If A = [3, 5, , 0 0, 3 0 ] , find 𝐴−1 by the adjoint method., 2 −1, , Q. 3. Solve the following equations by using inversion method., x + y + z = -1 , x - y + z = 2 and x + y - z = 3, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 10 :
PHOENIX INSTITUTE OF MATHEMATICS, Q. 4. If three numbers are added, their sum is 2. If 2 times the second number is, subtracted from the sum of first and third numbers, we get 8. If three times the first, number is added to the sum of second and third numbers, we get 4. Find the numbers, using matrices., 1, Q. 5. Find the inverse of A= [0, 1, 𝑥, Q. 6. If A = [0, 0, , 0 1, 2 3] by elementary column transformations., 2 1, , 0, 𝑦, 0, , 0, 0] is a non-singular matrix, then find 𝐴−1 by using, 𝑧, 2 0 0, elementary row transformations. Hence, write the inverse of [0 1 0 ]., 0 0 −1, cos 𝜃, Q. 7. Find the inverse of A = [ sin 𝜃, 0, transformations., 1, Q. 8. If A = [, 1, that AXB = C., , 4, 1, ], B = [, 2, 3, , − sin 𝜃, cos 𝜃, 0, , 0, 0], 1, , by using elementary row, , 1, 24 7, ], and C = [, ] , then find the matrix X such, 1, 31 9, , 1 −1, 2, Q. 9. If A = [3 0 −2] , verify that A(adj A) = (adj A)A., 1 0, 3, Q. 10. If A = [, , 1 0, 2 3, ], B = [, ], find AB and (𝐴𝐵)−1 ., 1 2, 3 1, , Q. 11. Solve the following system of equations by using inversion method., x+y=1, y+z=, , 5, 3, , and z + x =, , 4, 3, , Q. 12. The cost of 4 dozen pencils, 3 dozen pens and 2 dozen erasers is ₹ 60. The, cost of 2 dozen pencils, 4 dozen pens and 6 dozen erasers is ₹ 90. Whereas the cost of, 6 dozen pencils, 2 dozen pens and 3 dozen erasers is ₹ 70. Find the cost of each item, per dozen by using matrices., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 11 :
PHOENIX INSTITUTE OF MATHEMATICS, 3. TRIGONOMETRIC FUNCTIONS, I. MCQ (2 marks each ), , 1), , The principal solutions of √3 sec 𝑥 − 2 = 0 are _______., 𝜋 11𝜋, , a) ,, 3, , 2), , 3), , 6, , sin 𝐵, 2 sin 𝐶, , 6, , 3, , , then ∆𝐴𝐵𝐶 is _______., , d) an isosceles right angled triangle., , sin−1 𝑥 − cos −1 𝑥 =, , 𝜋, 6, , , then 𝑥 = _______., , 1, , b), , 2, , √3, , c) −, , 2, , 1, 2, , d) −, , √3, 2, , 1, , The principal value of sin−1 ( ) is _______., 2, 𝜋, , b), , 3, , 𝜋, , c), , 6, , 2𝜋, , d), , 3, , 3𝜋, 2, , 1, , The principal value of cos −1 (− ) is _______., 2, 𝜋, , b), , 3, , 𝜋, , c), , 6, , 2𝜋, , d), , 3, , 3𝜋, 2, , In ∆𝐴𝐵𝐶, if ∠𝐴 = 30°, ∠𝐵 = 60°, then the ratio of sides is _______., c) √3:1:2, , b) 2:√3:1, , d) √3:2:1, , In ∆𝐴𝐵𝐶, if 𝑏 2 + 𝑐 2 − 𝑎2 = 𝑏𝑐, then ∠𝐴 = _______., a), , 8), , 4, , c) an isosceles triangle., , a) 1:√3:2, , 7), , 4, , 𝜋 11𝜋, , d) ,, , b) a right angled triangle., , b), , 6), , 6, , 𝜋 11𝜋, , c) ,, , a) an equilateral triangle., , a), , 5), , 6, , In ∆𝐴𝐵𝐶, if cos 𝐴 =, , a), , 4), , 𝜋 11𝜋, , b) ,, , 𝜋, , b), , 4, , 𝜋, , c), , 3, 3 3𝜋, , If polar co-ordinates of a point are ( ,, 4, , 4, , 𝜋, , d), , 2, , 𝜋, 6, , ), then its Cartesian co-ordinate are, , _______., 3, , 3, , 3, , 3, , a) ( , − ) b) ( , ), 4√2, 4√2, 4√2 4√2, , c) (−, , 3, 4√2, , ,, , 3, , ), 4√2, , d) (−, , 3, 4√2, , ,−, , 3, , ), , 4√2, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 15 :
PHOENIX INSTITUTE OF MATHEMATICS, 5. Auxillary equation of 2𝑥 2 + 3𝑥𝑦 − 9𝑦 2 = 0 is….., A. 2𝑚2 + 3𝑚 − 9 = 0, , B. 9𝑚2 − 3𝑚 − 2 = 0, , C. 2𝑚2 − 3𝑚 + 9 = 0, , D. −9𝑚2 − 3𝑚 + 2 = 0, , 6. The combined equation of the lines through origin and perpendicular to the pair of, lines 3𝑥 2 + 4𝑥𝑦 − 5𝑦 2 = 0, is……., 5𝑥 2 + 4𝑥𝑦 − 3𝑦 2 = 0, , B. 3𝑥 2 + 4𝑥𝑦 − 5𝑦 2 = 0, , C. 3𝑥 2 − 4𝑥𝑦 + 5𝑦 2 = 0, , D. 5𝑥 2 + 4𝑥𝑦 + 3𝑦 2 = 0, , A, , 7.The acute angle between the lines represented by 𝑥 2 + 𝑥𝑦 = 0 is………., 𝜋, , A., , B., , 2, , 𝜋, , C., , 4, , 8 .If 2x+y=0 is one of the line represented by, , 𝜋, 6, , D., , 𝜋, 3, , 3𝑥 2 + 𝑘𝑥𝑦 + 2𝑦 2 = 0, , then k = …, A., , 1, , ., , 2, , B., , 11, 2, , C., , 2, 3, , D., , 3, 2, , II. Very Short Answers ( 2 mark ), 1) Find the combine equation of the pair of lines passing through the point (2,3), and parallel to the coordinate axes., 2) Find the separate equations of the lines given by 𝑥 2 + 2𝑥𝑦𝑡𝑎𝑛 ∝ −𝑦 2 = 0, 3) Find k, if the sum of the slopes of the lines represented by 𝑥 2 + 𝑘𝑥𝑦 − 3𝑦 2 =, 0, is twice their products., 4) Find the measure of acute angle between the lines given by 𝑥 2 − 4𝑥𝑦 + 𝑦 2 =, 0, 5) Find the value of h , if the measure of the angle between the lines 3𝑥 2 +, 2ℎ𝑥𝑦 + 2𝑦 2 = 0, is 450 ., III. Short Answers ( 3 marks ), 1) Find the combine equation of pair of lines passing through (-1,2), one is, parallel to x+3y-1=0 and other is perpendicular to 2x-3y-1=0., 2) Find the joint equation of pair of lines through the origin which are, perpendicular to the lines represented by 5𝑥 2 + 2𝑥𝑦 − 3𝑦 2 = 0, 3) Find the condition that the line 4x+5y=0 coincides with one of the lines given by, 𝑎𝑥 2 + 2ℎ𝑥𝑦 + 𝑏𝑦 2 = 0, 4) Find the measure of acute angle between the lines represented by 3𝑥 2 −, 4√3 𝑥𝑦 + 3𝑦 2 = 0, IV. Short answers ( 4 Marks), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 17 :
PHOENIX INSTITUTE OF MATHEMATICS, 6 ) The distance of the point (3, 4, 5) from Y- axis is _____, A)3, , B) 5, , C) √34, , D) √41, , 7) If cos α , cos β , cos γ are the direction cosines of a line then the value of, sin2 α + sin2 β + sin2 γ is ____, A)1, , B) 2, , C) 3, , D) 4, , 8) If |𝑎̅| = 2, |𝑏̅| = 5, 𝑎𝑛𝑑 𝑎̅. 𝑏̅ = 8 then |𝑎̅ − 𝑏̅| = ___, A) 13, , B) 12, , C) √13, , D) √21, , 9) If ̅̅̅̅, 𝐴𝐵 = 2𝑖̂ + 𝑗̂ − 3𝑘̂, and A( 1, 2 ,-1 ) is given point then coordinates of B are____, A) (3, 3, -4), , B) ( -3, 3 -2), , C) ( 3, 3, 2), , D) (-3, 3, 4), , 10) If l, m, n are direction cosines of a line then l𝑖̂ + 𝑚𝑗̂ + 𝑛𝑘̂ is ___, A ) Null vector, , B) the unit vector along the line., , C) Any vector along the line, , D) a vector perpendicular to the line., , 11) The values of 𝑐 that satisfy |𝑐 𝑢̅| = 3, 𝑢̅ = 𝑖̂ + 2𝑗̂ + 3𝑘̂ is ___, A) √14, , B) 3√14, , C), , 3, , D) 3, , √14, , 12. The value of î. ( ĵ × k̂ ) + ĵ. ( î × k̂ ) + k̂. ( î × ĵ ), A)0, , B) − 1, , 13. The two vectors ĵ + k̂ & 3î − ĵ + 4k̂, respectively of, A), , √34, 2, , C) 1, , D) 3, , represents the two sides AB and AC,, , a ABC. The length of the median through A is, B), , √48, 2, , C) √18, , D) √34, , II. Very Short Answers ( 1 mark ), 1. Find the magnitude of a vector with initial point : (1 , −3 , 4) ; terminal point, : (1 , 0 , −1)., 2. Find the coordinates of the point which is located Three units behind the YZplane, four units to the right of the XZ-plane and five units above the XYPlane., UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 20 :
PHOENIX INSTITUTE OF MATHEMATICS, 2. If Q is the foot of the perpendicular from P(2,4,3) on the line joining the points, A(1,2,4) and B(3,4,5), find coordinates of Q., 3. Prove that the angle bisectors of a triangle are concurrent., 4. Using vector method , find the incenter of the triangle whose vertices are, 𝐴(0,3,0), , 𝐵(0,0,4) and 𝐶(0,3,4)., , 5. Find the angles between the lines whose direction cosines 𝑙, 𝑚, 𝑛 satisfy the, equations 5𝑙 + 𝑚 + 3𝑛 = 0 and 5𝑚𝑛 − 2𝑛𝑙 + 6𝑙𝑚 = 0, 6. Let 𝐴(𝑎̅) and 𝐵(𝑏̅) be any two points in the space and 𝑅(𝑟̅ ) be a point on, the line segment 𝐴𝐵 dividing it internally in the ratio 𝑚 : 𝑛 then prove that, 𝑟̅ =, , 𝑚𝑏̅+𝑛𝑎̅, 𝑚+𝑛, , ., , 7. D and E divides sides BC and CA of a triangle ABC in the ratio 2 : 3, respectively. Find the position vector of the point of intersection of AD and BE, and the ratio in which this point divides AD and BE., 8. If u̅ = î − 2ĵ + k̂ , r̅ =3 î + k̂ & w, ̅ = ĵ , k̂ are given vectors , then find, [u̅ + w, ̅ ]. [( w, ̅ × r̅ ) × ( r̅ × w, ̅ )], 9. Find the volume of a tetrahedron whose vertices are, A( −1, 2, 3) 𝐵(3, −2, 1) ,C(2, 1, 3) and D( -1, -2, 4), 10.If four points A (a̅) , B(b̅) ,C(c̅) & D(d̅) are coplanar, then show that [a̅, , b̅, , d̅] + [b̅, , c̅, , d̅] + [c̅, , a̅, , d̅] = [a̅, , b̅, , c̅], , 6. LINE AND PLANE, I. Multiple choice questions…..( 2 marks ), 1)The equation of X axis is…, A) x = y= z (B)y = z (C) y = 0 ,z = 0 (D) x = 0 , y = 0, 2)If the perpendicular distance of the plane 2x+3y-z = k from the origin is √14 units, , then k = …, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 21 :
PHOENIX INSTITUTE OF MATHEMATICS, A) 14, , (B) 196, , (C) 2√14, , (D), , √14, 2, , 3) The equation of the plane passing through the points (1 ,-1 , 1 ) ,, ( 3 ,2 , 4 ) and parallel to Y axis is…, A)3x + 2z – 1 = 0, , (B) 3x – 2z = 1 (C) 3x+2z+1 = 0 (D)3x+2z = 2, , 4)The direction ratios of the line 3x+1 = 6y –2 = 1 – z are, A)2 ,1 ,6 (B)2 ,1 ,-6 (C)2 ,-1 , 6 (D) -2,1 ,6, 5)If the planes 2x – my + z = 3 and 4x – y + 2z = 5are parallel then m = …, A)– 2, , (B) 2, , (C), , −1, , (D), , 2, , 1, 2, , 6) The direction cosines of the normal to the plane 2x – y + 2z = 3 are, 2, , A) ,, 3, , −1 2, , ,, , 3, , (B), , 3, , −2, 3, , 1 −2, , , ,, , 3 3, , (C) 2 , -1 ,2 (D) -2 ,1 ,-2, , 7)If the foot of the perpendicular drawn from the origin to the plane is (4 ,-2 ,5) , then, the equation of plane is…, A)4x+y+5z = 14 (B) 4x-2y-5z = 45 (C) x-2y-5z =10 (D)4x+y+6z=11, 8)The perpendicular distance of the origin from the plane x-3y+4z=6 is…., A) 6, , (B), , 6, √26, , (C) 36, , (D), , 1, √26, , 9)The coordinates of the foot of perpendicular drawn from the origin to the plane, 2x+y-2z = 18 are…, A)(4 ,2 ,4) (B) (-4 ,2 ,4) (C) (-4 ,-2 ,4) (D) (4 ,2 ,-4), II. Very Short answers, , (1 marks ), , 1)Find the Cartesian equation of a plane passing through A(1 ,2 ,3) and direction, ratios of it’s normal are 3 ,2 ,5., 2)Find the direction ratios of the normal to the plane 2x+3y+z=7., 3)Find the vector equation of the line, 𝑥, 1, , =, , 𝑦−1, 2, , =, , 𝑧−2, 3, , 4)Verify if the point having position vector 4𝑖̂-11𝑗̂+2𝑘̂ lies on the line, 𝑟̅ = (6𝑖̂-4𝑗̂+5𝑘̂) + µ (2𝑖̂ +7𝑗̂+3𝑘̂) ,, 5)Find the Cartesian equation of the line passing through, A (1 ,2 ,3)and having direction ratios 2,3,7., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 22 :
PHOENIX INSTITUTE OF MATHEMATICS, 6)Find the vector equation of the line passing through the point having position, vector 4𝑖̂ - 𝑗̂+2𝑘̂ and parallel to the vector -2𝑖̂ -𝑗̂+𝑘̂., , 7)Find the Cartesian equation of the plane passing through the points (3 ,2 ,1) and (1, ,3 ,1), III Short answer questions, , ( 2 marks ), , 1) Find the direction ratios of the line perpendicular to the lines, 𝑥−7, 2, , =, , 𝑦+7, −3, , =, , 𝑧−6, 1, , and, , 𝑥+5, 1, , =, , 𝑦+3, 2, , =, , 𝑧−6, −2, , 2)Find direction cosines of the normal to the plane 𝑟̅ .(3𝑖̂+4𝑘̂) = 5, 3)If the normal to the plane has direction ratios 2 ,-1 ,2 and it’s perpendicular, distance from origin is 6 ,find its equation., 4)Reduce the equation 𝑟̅ . (3𝑖̂ + 4𝑗̂ + 12𝑘̂) 6767 =8 to normal form., 5) Find the Cartesian equation of the line passing through A(1 ,2 ,3) and, B (2, 3, 4), 6)Find the perpendicular distance of origin from the plane 6x-2y+3z -7=0, 7)Find the acute angle between the lines x=y ; z=0 and x=0 z=0., , IV. Short answer questions, , (3 marks ), , 1)Find Cartesian equation of the line passing through the point A(2 ,1 ,-3) and, perpendicular to vectors 𝑖̂+𝑗̂+𝑘̂ and 𝑖̂+2𝑗̂-𝑘̂, 2)Find the vector equation of the line passing through the point having position, vector -𝑖̂ -𝑗̂+2𝑘̂ and parallel to the line 𝑟̅ =( 𝑖̂+2𝑗̂+3𝑘̂ )+ µ (3𝑖̂+2𝑗̂+𝑘̂ ) ;µ is a, parameter., 3)Find the Cartesian equation of the line passing through (-1 ,-1 ,2) and parallel to the, line 2x-2 = 3y+1 = 6z – 2., 4)Find the Cartesian equation of the plane passing through A(7 ,8 ,6)and parallel to, XY plane., 5)Find the coordinates of the foot of perpendicular from the origin to the plane, 2x+6y -3z =63., 6)Find the vector equation of a plane at a distance 6 units from the origin and to, which vector 2𝑖̂-𝑗̂+2𝑘̂ is normal., 7)Find the Cartesian equation of the plane passing through the points A( 1 ,1 ,2),, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 23 :
PHOENIX INSTITUTE OF MATHEMATICS, B(0 ,2 ,3) C(4 ,5 ,6)., 𝑥−1, , 8)Find acute angle between the lines, , 1, , =, , 𝑦−2, −1, , =, , 𝑥, , 9)Find the distance between the parallel lines, , 𝑧−3, 2, 𝑦, , =, , 2, , −1, , 𝑥−1, , and, =, , 2, , 𝑧, , and, , 2, , =, , 𝑦−1, , 𝑥−1, 2, , 1, , =, , =, , 𝑧−3, , 𝑦−1, −1, , 1, , =, , 𝑧−3, 2, , ., , 10)Find the equation of the plane passing through the point (7 ,8 ,6) and parallel to, the plane 𝑟̅ .(6𝑖̂ + 8𝑗̂+7𝑘̂) =0, 11)Find m, if the lines, , 1−𝑥, 3, , =, , 7𝑦−14, 2𝑚, , =, , V. Long answer questions, 1) show that the lines, , 𝑥+1, −10, , =, , 𝑧−3, 2, , and, , 7−7𝑥, 3𝑚, , =, , 𝑦−5, 1, , =, , 6−𝑧, 5, , are at right angles., , (4 marks), 𝑦+3, −1, , =, , 𝑧−4, 1, , and, , 𝑥+10, −1, , =, , 𝑦+1, −3, , =, , 𝑧−1, 4, , intersect each other.also, , find the coordinates of the point of intersection., 2)A(-2 ,3 ,4) B(1 ,1 ,2) C(4 ,-1 ,0) are three points. Find the Cartesian equation of line, AB and show that points A, B ,C are collinear., 3)find the Cartesian and vector equation of the line passing through the point having, position vector 𝑖̂+2𝑗̂ +3𝑘̂ and perpendicular to vectors 𝑖̂+𝐽̂+𝑘̂ and 2𝑖̂-𝑗̂+𝑘̂., 4)Find the vector equation of the plane which bisects the segment joining A(2 ,3 ,6), and B (4 ,3 ,-2) at right angles., 5)Find vector equation of the plane passing through A(-2 ,7 ,5)and parallel to vectors, 4𝑖̂ -𝑗̂+3𝑘̂ and 𝑖̂+𝑗̂ +𝑘̂., 6)Find the Cartesian and vector equation of the plane which makes intercepts 1 ,1 ,1, on the coordinate axes., , 7. LINEAR PROGRAMMING PROBLEMS, I. MCQ (2 marks each ), 1. The corner points of the feasible solutions are (0,0) (3,0) (2,1) (0,7/3) the, maximum value of Z = 4x+5y is, a) 12, , b) 13 c) 35/3, , d) 0, , 2. The half plane represented by 4x+3y >14 contains the point, a) (0,0), , b) (2,2) c) (3,4), , b) (1,1), , 3. The feasible region is the set of point which satisfy, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 24 :
PHOENIX INSTITUTE OF MATHEMATICS, a) The object functions, b) All the given constraints, c) Some of the given constraints, d) Only one constraint, 4. Objective function of LPP is, a) A constraint, b) A function to be maximized or minimized, c) A relation between the decision variable, d) Equation of straight line, 5. The value of objective function is maximum under linear constraints, a) At the center of the feasible region, b) At (0,0), c) At vertex of feasible region, d) At (-1, -1), 6. If a corner point of the feasible solutions are (0,10) (2,2) (4,0) (3,2) then the, point of minimum Z = 3x + 2y is, a) (2,2), , b) (0,10), , c) (4,0), , b) (3,2), , 7. The point of which the maximum value of z= x+y subject to constraints, x+2y≤70, 2x+y ≤ 90, x≥0, y≥0 is obtained at, a) (30,25), , b) (20,35), , c) (35,20), , b) (40,15), , 8. A solution set of the inequality x ≥ 0, a) Half plane on the Left of y axis, b) Half plane on the right of y axis excluding the point on y-axis, c) Half plane on the right of y axis including the point on y axis, d) Half plane on the upword of x axis, 9. Which value of x is in the solution set of inequality -2X+Y ≥ 17, a) - 8, , b) -6 c) -4, , b) 12, , 10.The graph of the inequality 3X- 4Y ≤ 12, X≤ 1, X ≥ 0, Y ≥ 0 lies in fully in, a) I quadrant b) II quadrant, , c) III quadrant, , b) IV quadrant, , II. Short Answers ( 2 marks ), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 25 :
PHOENIX INSTITUTE OF MATHEMATICS, 1. Solve 4x-18 ≥ 0 graphically using xy plane, 2. Sketch the graph of inequation x ≥ 5y in xoy co-ordinate system, 3. Find the graphical solution for the system of linear inequation 2x+y ≤ 2, x-y≤ 1, 4. Find the feasible solution of linear inequation 2x+3y ≤ 12, 2x+y ≤ 8,, x ≥ 0, y≥ 0 by graphically, 5. Solve graphically x ≥ 0, y ≥ 0, 6. Find the solution set of inequalities 0 ≤ x ≤ 5, 0 ≤ 2y ≤ 7, 7. Find the feasible solution of in equations 3x+2y ≤ 18, 2x+ y ≤ 10, X ≥ 0,, Y≥0, 8. Draw the graph of inequalities x ≤ 6, y- 2 ≤ 0, x ≥ 0, y ≥ 0 and indicate the, feasible region, 9. Check the ordered points (1, - 1), (2, - 1) is a solution of 2x+3y-6 ≤ 0, 10.Show the solution set of inequations 4x – 5y ≤ 20 graphically, , III. Long Answers ( 4 marks ), 1. Maximize z = 5x+2y subject to 3x+5y ≤ 15, 5x+2y ≤ 10, x ≥ 0, y ≥ 0, 2. Maximize z= 7x+11y subject to 3x+5y ≤ 26, 5x+3y ≤ 30, x ≥ 0, y ≥ 0, 3. Maximize z=10x+25y subject to x+y ≤ 5, 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, 4. Maximize z=3x+5y subject to x+4y ≤ 24, 3x+y≤ 21, x+y≤ 9, x ≥ 0, y ≥ 0 also, find the maximum value of z, 5. Minimize z=8x+10y subjected to 2x+y ≥ 7, 2x+3y≥15, y≥2, x ≥ 0, y ≥ 0, 6. Minimize z=7x+y subjected to 5x+y ≥ 5, x+y ≥ 3, x ≥ 0, y ≥ 0, 7. Minimize z= 6x+21y subject to x+2y≥ 3, x+ 4y≥ 4, 3x+y ≥ 3, x ≥ 0, y ≥ 0, show that the minimum value of z occurs at more than two points, 8. minimize z =2x+4y is subjected to 2x+y≥3, x+2y≥6, x≥ 0, y≥ 0 show that the, minimum value of z occurs at more than two points, 9. Maximize z=-x+2y subjected to constraints x+y≥ 5, x≥3, x+2y ≤ 6, y ≥ 0 is this, LPP solvable? Justify your answer, 10.x-y ≤ 1, x - y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x, + y. It is solvable for finding optimum value of z? Justify?, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 26 :
PHOENIX INSTITUTE OF MATHEMATICS, Part 2, 1. DIFFERENTIATION, I. MCQ (2 Marks each), , 1) If y = sec (tan-1 x) then, (a), , 1, 2, , dy, at x = 1 is _____, dx, , (c) 1, , (b) 1, , (d), , 2, , 2, , 2) If f(x) = logx (log x) then f (e) is _____, (a)1, , (b) e, , 3) If y  25, , log5 sin x, , (a)1, , (c), , 1, e, , (d) 0, ,  16 log4 cos x, , (b) 0, , then, , dy,  ____, dx, , (d) cos x – sin x, , (c) 9, , 4) If f (4)  5, f (4)  3, g (6)  7 and R(x) = g[3 + f(x)] then R(4)  _____, (b) 12 (c) 7 5, , (a)35, , (d) 105, , , 5) If y  tan 1 , , 2x , dy,  ______ ., 2  , x  (1,1) then, dx, 1 x , , (a), , 2, 1 x2, , (b) 1, , (c), , 6) If g is the inverse of f and f ( x) , (a), , 1, 1  [ g ( x)]4, , 4x3, (b), 1 x4, , 7) If sin-1 (x3 + y3) = a then, (a), , (b) – t, , 9), , 1, 1 x2, , 1, 1  [ g ( x)]3, , (d) 1  [ g ( x)] 4, , dy,  ______, dx, , 8) If x = cos-1 (t), y  1  t 2 then, (a) t, , (d), , 1, then g ( x)  ______, 1 x4, , (c), ,  x2, (b) 2, y, , x, cos a, , 2, 1 x2, , (c), , y2, x, , 2, , (d), , sin a, y, , dy,  ______, dx, , (c)  1t, , (d) 1t, , d 2x, If x + y = 1 then 2  ______ ., dy, 2, , 2, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 28 :
PHOENIX INSTITUTE OF MATHEMATICS, IV. Short answer questions ( 3 mark each), ,  , dy, , find, , dx,  , , 1), ,  1  cos 3x, 2, If y  log , 1  cos 3x, 2, , , 2), , 3,   2, 2, , x, , 5, 2x, ,  , find dy, , , y, , log, 4, If, , , 3,   2x  4  , dx, , , , , 3) Differentiate cot 1 , , cos x ,  w.r. to x,  1  sin x , ,  2 cos x  3 sin x ,  w.r. to x, 13, , , , 4) Differentiate sin 1 , , , 5) Differentiate tan 1 , , 8x , 2  w.r. to x,  1  15 x , , 6), ,  x4  y4 , dy 12 x 3, , ,  2 , show that, , If log 5  4, 4 , dx 13 y 2, x y , , 7) If y  cos x  cos x  cos x  ..... , show that, , dy sin x, , dx 1  2 y, , 8) Find the derivative of cos-1x w.r. to 1  x 2, 9) If x sin(a + y) + sin a cos (a + y) = 0 then show that, 10) If y = 5x . x5 . xx . 55, find, , dy sin 2 (a  y ), , dx, sin a, , dy, dx, , V. Long answer questions ( 4 mark each), , 1) If y  e, , m tan1 x, , d2y, dy, , show that (1  x ) 2  (2 x  m)  0, dx, dx, 2, , 2) If x7 . y5 = (x + y)12, show that, 3), , dy y, , dx x, , 2,  1  x2 1, , 1  2 x 1  x, , , tan, Differentiate tan ,  w.r. to,  1  2x 2, x, , , , 1, , , , , , ,  a cos x  b sin x ,  then find dy, , dx, a2  b2 , , , 4) If y  sin 1 , , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 29 :
PHOENIX INSTITUTE OF MATHEMATICS, 5), , If y = cos (m cos x) then show that (1  x 2 ), -1, , d2y, dy,  x  m2 y  0, 2, dx, dx, , :: Theorems ::, , 1) If y = f(u) is a differentiable function of u and u = g(x) is a differentiable, function of x such that the composite function y = f[g(x)] is a differentiable, function of x then, , dy dy du,  ., dx du dx, , Hence find, , dy, if y = sin2 x, dx, , 2) Suppose y = f(x) is a differentiable function of x on an interval I and y is oneone, onto and, , dy,  0 on I. Also if f ( y ) is differentiable on f(I) then, dx, , dx, 1, , , dy dx  0, dy dy, dx, , 3) If x = f(t) and y = g(t) are differentiable functions of t so that y is a, dy, dy dt, , differentiable function of x and it dx dt  0 then, ., dx dx, dt, , 2. APPLICATIONS OF DERIVATIVE, I. MCQ (2 Marks each), 𝜋, , 1. The slope of the tangent to the curve x = 2 sin3θ, y = 3 cos3 θ at θ = is, 4, , (A), , 3, 2, , (B) −, , 3, 2, , 2, , (C), , 3, , (D) −, , 2, 3, , 2. The slope of the normal to the curve 𝑦 = 𝑥 2 + 2𝑒 𝑥 + 2 at (0,4) is, (A), , 2, , (B) −2, , (C), , 1, 2, , (D) −, , 1, 2, , 3. If the line y = 4x – 5 touches the curve y2 = ax3 + b at the point (2, 3) then a + b is, (A) −5, , (B), , 2, , (C) −7, , (D) 9, , 4. If the tangent at ( 1, 1) on 𝑦 2 = 𝑥 ( 2 − 𝑥)2 meets the curve again at P, then P is, (A), , (4,4), , (B)(-1, 2), , (C) ( 3, 6), , (D), , 9 3, , (4 , 8), 5. The displacement of a particle at time t is given by s = 2t3 – 5t2 + 4t – 3. The time, when the acceleration is 14 ft/sec2, is, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 30 :
PHOENIX INSTITUTE OF MATHEMATICS, (A) 1 sec, , (B) 2 sec, , (C) 3 sec, , (D) 4 sec, , 6. Let 𝑓(𝑥) = 𝑥 3 − 62 + 9𝑥 + 18, then 𝑓(𝑥) is strictly decreasing in …, (A) (-∞, 1), , (B) [3,∞), , (C) (-∞, 1) ∪[3,∞), , (D) (1, 3), , 7. A ladder 5 m in length is resting against vertical wall. The bottom of the ladder is, pulled along the ground, away from the wall at the rate of 1.5 m /sec. The length, of the higher point of the when foot of ladder is 4 m away from the wall, decreases at the rate of ___, (A), , 1, , (B) 2, , (C) 2.5, , D) 3, , 8. The edge of a cube is decreasing at the rate of 0.6 cm/sec then the rate at which its, volume is decreasing when the edge of the cube is 2 cm, is, (A) 1.2 cm3 /sec (B) 3.6 cm3 /sec, , (C), , 4.8 cm3 /sec, , (D) 7.2 cm3, , /sec, 9., , A particle moves along the curve 𝑦 = 4𝑥 2 + 2, then the point on the curve at, , which y – coordinate is changing 8 times as fast as the x – coordinate is, (A) (2,18), , (B) (−1,6), , (C) (1,6), , (D) (0,2), , 10. The function 𝑓(𝑥) = 𝑥 𝑙𝑜𝑔 𝑥 is minimum at 𝑥 =, (A), , 𝑒, , (B), , 1, 𝑒, , (C), , (D) −, , 1, , 1, 𝑒, , II. Very Short answer questions ( 1 mark each), 1, , 1. Find the slope of tangent to the curve y = 2x3 – x2 + 2 at ( , 2)., 2, 2. The displacement of a particle at time t is given by s = 2t3 – 5t2 + 4t – 3.Find the, velocity when 𝑡 = 2 sec., 1, , 3. Prove that function f(x) = x - , x ∈ R and x≠ 0 is increasing function., 𝑥, , 4. Show that f(x) = x – cos x is increasing for all x., 5. Show that the function 𝑓(𝑥) = 𝑥 3 + 10𝑥 + 7 for 𝑥 ∈ 𝑅 is strictly increasing., III. Short answer questions ( 2 mark each), 1. Find the slope of normal to the curve 3𝑥 2 − 𝑦 2 = 8 at the point (2,2)., 𝜋, , 2. Find the slope of tangent to the curve 𝑥 = 𝑠𝑖𝑛𝜃 and 𝑦 = 𝑐𝑜𝑠2𝜃 at 𝜃 = ., 6, , 1, , 3. Find the equation of normal to the curve y = 2 x3 – x2 + 2 at ( , 2), 2, , 4. A car is moving in such a way that the distance it covers, is given by the equation, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 31 :
PHOENIX INSTITUTE OF MATHEMATICS, s = 4t2 + 3t ,where s is in meters and t is in seconds. What would be the velocity, and the acceleration of the car at time t = 20 second ?, 5. A man of height 2 meters walks at a uniform speed of 6 km/hr away from a lamp, post of 6 meters, , high. Find the rate at which the length of the shadow is, , increasing, 6. Water is being poured at the rate of 36 m3/sec in to a cylindrical vessel of base, radius 3 meters. Find the rate at which water level is rising., 7. Test whether the function 𝑓(𝑥) = 𝑥 3 + 6𝑥 2 + 12𝑥 − 5 is increasing or decreasing, for all 𝑥 ∈ 𝑅., 8. Test whether the following function f(x) = 2 – 3x +3x2 – x3 , x ∈ R is increasing or, decreasing., 9. Find the values of x for which the function f(x) = 2x3 – 6x2 + 6 x + 24 is strictly, increasing., IV. Short answer questions ( 3 mark each), 1. Find the point on the curve 𝑦 = √𝑥 − 3 where the tangent is perpendicular to, the line 6x + 3y – 5 = 0., 2. A spherical soap bubble is expanding so that its radius is increasing at the rate, of 0.02 cm/sec. At what rate is the surface area is increasing, when its radius is, 5 cm?, 3. The surface area of a spherical balloon is increasing at the rate of 2 cm2/sec., At what rate the volume of the balloon is increasing when radius of the balloon, is 6 cm?, 4. A ladder 10 meter long is leaning against a vertical wall. If the bottom of the, ladder is pulled horizontally away from the wall at the rate of 1.2 meters per, seconds, find how fast the top of the ladder is sliding down the wall when the, bottom is 6 meters away from the wall., 5. Find the values of x for which the function f(x) = x3 – 6x2 -36x +7 is strictly, increasing., 6. Find the values of x, for which the function f (x) =𝑥 3 + 12𝑥 2 + 36𝑥 + 6 is, monotonically decreasing., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 32 :
PHOENIX INSTITUTE OF MATHEMATICS, 7. The profit function P(x) of a firm, selling x items per day is given by 𝑃(𝑥) =, (150 − 𝑥)𝑥 − 1625. Find the number of items the firm should manufacture to, get maximum profit. Find the maximum profit., 8. Divide the number 30 in to two parts such that their product is maximum., 9. A wire of length 36meters is bent in the form of a rectangle. Find its dimensions if, the area of the rectangle is maximum., V. Long answer questions ( 4 mark each), 1. Find points on the curve given by 𝑦 = 𝑥 3 − 6𝑥 2 + 𝑥 + 3 where the tangents are, parallel to the line 𝑦 = 𝑥 + 5., 2. The volume of the spherical ball is increasing at the rate of 4π cc/sec. Find the, rate at which the radius and the surface area are changing when the volume is, 288πcc., 3. The volume of a sphere increase at the rate of 20 cm3/sec. Find the rate of change, of its surface area when its radius is 5 cm., 4. A man of height 180 cm is moving away from a lamp post at the rate of 1.2, meters per second. If the height of the lamp post is 4.5 meters, find the rate at, which, (i) his shadow is lengthening. (ii)the tip of the shadow is moving., 5. Find the values of x for which f(x) =2 x3 – 15x2 -144x -7 is, (a) Strictly increasing, , (b) strictly decreasing, , 6. Find the local maximum and local minimum value of, 𝑓(𝑥) = 𝑥 3 − 3𝑥 2 − 24𝑥 + 5., 7. A wire of length 120cm is bent in the form of a rectangle. Find its dimensions if, the area of the rectangle is maximum., 8. An open box is to be cut out of piece of square card board of side 18 cm by, cutting of equal squares from the corners and turning up the sides. Find the, maximum volume of the box., 9. A rectangular sheet of paper has it area 24 sq. Meters. The margin at the top &, the bottom are 75cm each & the sides 50cm each. What are the dimensions of the, paper if the area of the printed space is maximum?, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 42 :
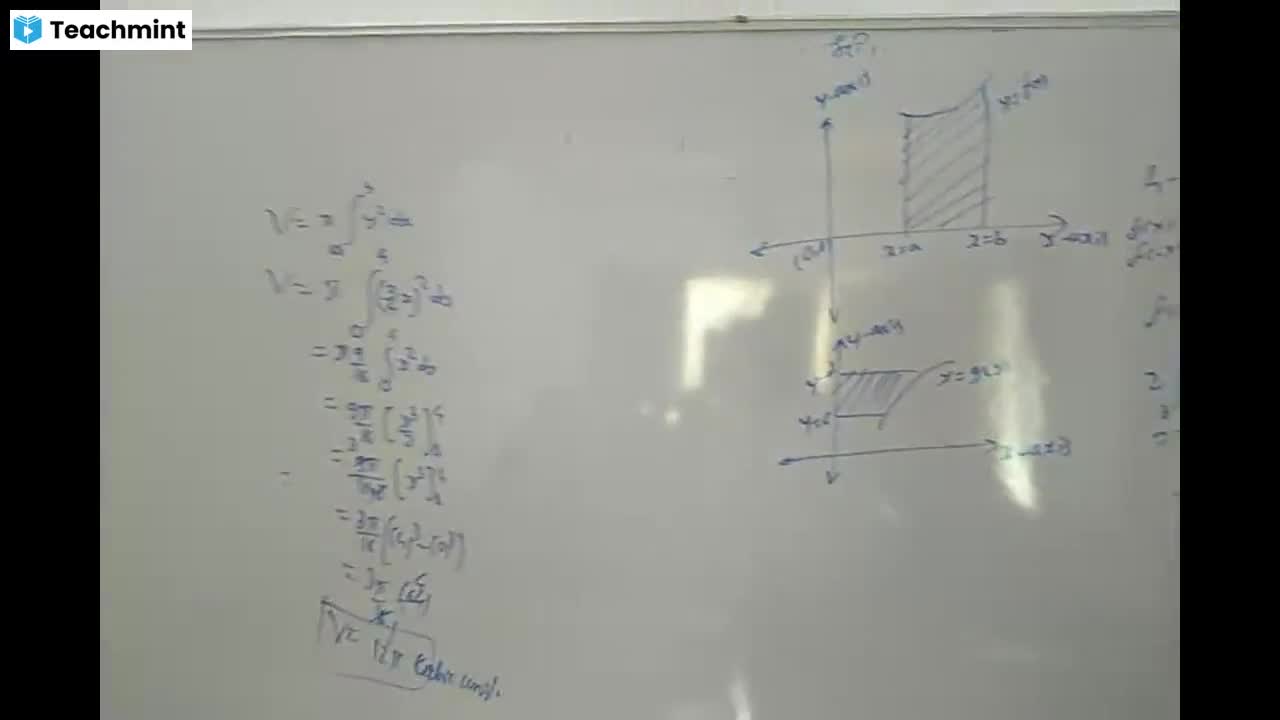
PHOENIX INSTITUTE OF MATHEMATICS, 𝜋, , (53) Evaluate: ∫0 𝑥 ∙ 𝑠𝑖𝑛𝑥 ∙ 𝑐𝑜𝑠 2 𝑥 ∙ 𝑑𝑥, 𝜋, 2, , (54) Evaluate: ∫0 𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥, 1 1+𝑥 3, , (55) Evaluate: ∫−1, , 9−𝑥 2, , 1, , 𝑑𝑥, , 1, , 2𝑥, , (56) Evaluate: ∫0 ( 2 ) sin−1 ( 2) 𝑑𝑥, 1+𝑥, 1+𝑥, 𝜋, , (57) Evaluate: ∫04, , 𝑐𝑜𝑠2𝑥, 1+cos 2𝑥+sin 2𝑥, , 𝜋/4, , (58) Evaluate: ∫0, , 𝜋, , (59) Evaluate: ∫0, , 𝑑𝑥, , 𝑙𝑜𝑔 (1 + 𝑡𝑎𝑛𝑥) 𝑑𝑥, 1, , 3 + 2𝑠𝑖𝑛𝑥 + 𝑐𝑜𝑠𝑥, , 𝑑𝑥, , 5. APPLICATION OF DEFINITE INTEGRATION, , I. MCQ (2 marks each ), Ex.1: The area of the region bounded by the curve y = sinx , X-axis and, the lines x = 0, x = 4π is …… sq. units., (A) 2, (B) 4, (C) 8, (D) 16, 2, Ex.2: The area of the region bounded by the ellipse x /64 + y2/100 = 1,, is …….. sq. units., (A)64 , , (B) 80, , (C) /80, , (D) 100, , Ex.3: The area bounded by the parabola y2 = x along the X- axis &, the lines x =0 , x= 2 is …… sq. units., (A) 4/3, (B) (4√2)/3, (C) 2/3, (D) (2√2)/3, 2, 2, Ex.4: The area bounded by the curve y = x , and the line x = 8 is ……, (A)16 sq. units (B) 64 sq. units (C) 32 sq. units (D) 4 sq. units, Ex.5: The area of the region included between the parabolas y2 = 16x, and x2 = 16y, is given by …….. sq.units, (A) 256 (B) 16/3, (C) 256/3, (D) 64/3, 2, Ex.6: The area enclosed between the two parabolas y = 20x, and y = 2x is ….. sq. units., (A) 20/3, (B) 40/3, (C) 10/3, (D) 50/3, 2, Ex.7: The area bounded by the parabola y = 32x the X-axis and, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 43 :
PHOENIX INSTITUTE OF MATHEMATICS, the latus rectum is …….. sq. units, (A), 512/3, (B) 512/5 (C) 512, (D) 64/3, 2, 2, Ex.8: The area bounded by the ellipse x /4 + y /25 = 1 & and, the line x/2 + y/5 = 1 is ……. sq. units, (A) 5(-2), (B) (5/2) (-2), (C) (5/3)(-2), (D) (5/4)(-2), Ex.9: The area of triangle ABC whose vertices are A(1,1) ,B(2,1) &, C(3,3) is …….sq. units., (A) 1, (B) 2, (C) 3, (D) 4, Ex.10: The area enclosed by the line 2x + 3y = 6 along X-axis &, the lines x = 0 , x = 3 is ……… sq. units., (A), , 1, , (B) 2, , (C) 3, , (D) 4, , II. Very Short Answers ( 1 mark ), Ex. 1 : Find the area bounded by the curve y2 = 36x, the line x = 2, in first quadrant ., Ex.2: Find the area bounded by the curve y = sinx , the lines x = 0 and x = /2., Ex.3: Find the area enclosed between y = cos x and X-axis between the, lines x = /2 & x ≤ 3/2, Ex.4: Find the area of the region bounded by the parabola y2 = 32x and, its Latus rectum in first quadrant ., Ex.5: Find the area of the region bounded by the curve y = x2 , the, X−axis and the given lines x = 0 , x = 3, Ex.6: Find the area of the region bounded by the curve y2 = 8x, the, X−axis and the given lines x = 1, x = 3, y ≥ 0, Ex.7: Find the area of the region bounded by the curve x2 = 12y, the, Y−axis and the given lines y = 2, y = 4, x ≥ 0, Ex.8: Find the area of the ellipse x2 /1 + y2 / 4 = 1 , in first quadrant, Ex.9: Find the area of sector bounded by the circle x2 + y2 = 25 ,, in the first quadrant., Ex.10: Using integration, find the area of the region bounded by the line, 2y + x = 8 , X−axis and the lines x=2 & x = 4., III. Short Answers ( 3 marks ), Ex.1: Find the area enclosed between the X-axis and the curve y = sin x, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 44 :
PHOENIX INSTITUTE OF MATHEMATICS, for values of x between 0 to 2 ., Ex.2: Find the area of the region bounded by the parabola x2 = 4y and, The X-axis & the line x = 1, x = 4., Ex.3: Find the area of the region bounded by the parabola y2 = 16x and, the line x = 4., Ex.4: Find the area of the region bounded by the curves, x2 = 8y, y = 2, y = 4 and the Y-axis, lying in the first quadrant., Ex.5: Find the area of the region bounded by the curve y = sin x,, the X−axis and the given lines x = -  , x = , Ex.6: Find the area of the ellipse x2 /36 + y2 / 64 = 1, using integration., , IV. Long answers ( 4 Marks), Ex.1 : Find the area of the region bounded by the curves y2 = 4ax, and x2 = 4ay., Ex.2: Find the area of the region lying between the parabolas, 4y2 = 9x and 3x2 = 16y, Ex.3: Find the area of the sector bounded by the circle x2+ y2 = 16 ,, & the line y = x in the first quadrant., Ex.4: Find the area of the region included between y = x2 + 5 and, the line y = x + 7, Ex.5: Find the area enclosed between the circle x2 + y2 = 9 ,, along X – axis and the line x = y , lying in the first quadrant., Ex.6: Find the area enclosed between the circle x2 + y2 = 1 and, the line x + y = 1, lying in the first quadrant., Ex.7: Find the area of the region bounded by the curve, ( y − 1)2 = 4 (x + 1) and the line y = (x − 1)., , 6. DIFFERENTIAL EQUATIONS, I., , Select & write the correct alternative from the given option, for each question (2 Marks), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 48 :
PHOENIX INSTITUTE OF MATHEMATICS, 7. Solve the following differential equation, 𝑦 𝑙𝑜𝑔𝑦, , 𝑑𝑦, 𝑑𝑥, , = 𝑙𝑜𝑔𝑦 − 𝑥, , 8. For the differential equation, find the particular solution, 𝑑𝑦, , = (4𝑥 + 𝑦 + 1), when 𝑦 = 1, 𝑥 = 0, , 𝑑𝑥, , 9. Solve the following differential equation, 𝑦 2 𝑑𝑥 + (𝑥𝑦 + 𝑥 2 )𝑑𝑦 = 0, 10., , Solve the following differential equation, 𝑥2, , 𝑑𝑦, 𝑑𝑥, , = 𝑥 2 + 𝑥𝑦 − 𝑦 2, , 7. PROBABILITY DISTIBUTIONS, I. MCQ (2 marks each ), (i) Let the p.m.f. of a random variable X be, P (x) =, , 3−𝑥, 10, , , for x = -1 ,0,1,2, , = 0 , otherwise, Then E (X) is ….., (A) 1, , (B) 2, , (C) 0, , (D) -1, , (ii) c.d.f of a discrete random variable X is, (A) an identity function., , (B) a step function., , (B) an even function., , (D) an odd function., , (iii) If X denotes the number on the uppermost face of cubic die when, it is tossed, then E(x) is …., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 49 :
PHOENIX INSTITUTE OF MATHEMATICS, (A), , 2, , (B), , 7, , 7, , (C) 1, , 2, , (D), , 1, 2, , (iv) A random variable X has the following probability distribution, X, , 2, , 3, , 4, , P(x), , 0.3, , 0.4, , 0.3, , Then the variance of this distribution is, (A) 0.6, , (B) 0.7, , (C) 0.77, , (D) 0.66, , (v) For the random variable X , if V(X) = 4 , E(X) = 3 , then E(𝑋 2 ) is …, (A) 9, , (B) 13, , (c) 12, , (D) 7, , (vi) If a d.r.v. X takes values 0, 1, 2, 3, . . . with probability, 𝑃(𝑋 = 𝑥) = 𝑘(𝑥 + 1) × 5−𝑥 , where 𝑘 is a constant then 𝑃(𝑋 = 0) =…, (A), , 7, 25, , ( B), , 16, , (C ), , 25, , (vii) The p.m.f of a d.r.v. X is 𝑃(𝑋 = 𝑥) =, , 18, , (D), , 25, 5, ( ), 𝑥, { 25 , for, , 19, 25, , 𝑥 = 0, 1, 2, 3 ,4, 5, , 0, otherwise, If 𝑎 = 𝑃(𝑋 ≤ 2) and 𝑏 = 𝑃(𝑋 ≥ 3) then, (A) 𝑎 < 𝑏, , (B) 𝑎 > 𝑏, , (C) 𝑎 = 𝑏, 𝑥, , (viii) If the p.m.f of a d.r.v. X is 𝑃(𝑋 = 𝑥) = {𝑛(𝑛+1), , (D) 𝑎 + 𝑏 = 2, , , for 𝑥 = 1, 2, 3 , … , 𝑛, 0, otherwise, , 𝐸(𝑋) = ⋯, UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 ), , then

Page 50 :
PHOENIX INSTITUTE OF MATHEMATICS, (A) 𝑛 +, , 1, , 𝑛, , 1, , 3, , 6, , (B) +, , 2, , 𝑛, , 1, , 2, , 5, , (C) +, 𝑐, , (ix) If the p.m.f of a d.r.v. X is 𝑃(𝑋 = 𝑥) = {𝑥 3, , (D) 𝑛 +, , 1, 3, , , for 𝑥 = 1, 2, 3, 0, otherwise, , then 𝐸(𝑋) = ⋯, (A), , 343, , (B), , 297, , 294, , (C), , 251, , 297, , (D), , 294, , 294, 297, , (x) If a d.r.v. X has the following probability distribution :, X, −2, −1, 0, k, 0·2, P(𝑋=𝑥) 0·1, then 𝑃(𝑋 = −1) is …, (A), , 1, , (B), , 10, , 1, 2k, , 2, , 2, 0·3, , (C), , 10, , 3, k, , 3, , (D), , 10, , 4, 10, , (xi) If a d.r.v. X has the following probability distribution:, X, , 1, , 2, , 3, , 4, , 5, , P(𝑋=𝑥), , k, , 2k, , 2k, , 3k, , k2, , 6, , 7, , 2 k2 7k2+k, , then 𝑘 = …, (A), , 1, 7, , (B), , 1, 8, , (C), , 1, 9, , (D), , 1, 10, , II. Very Short Answers ( 1 mark ), 1. Let X represent the difference between number of heads and number of tails, obtained when a coin is tossed 6 times. What are possible values of X?, 2. An urn contains 5 red and 2 black balls. Two balls are drawn at random. X, denotes number of black balls drawn. What are possible values of X?, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 51 :
PHOENIX INSTITUTE OF MATHEMATICS, 3. State which of the following are not probability mass function of random, variable.Give reasons of your answers., X, , 0, , 1, , 2, , P(X), , 0.4, , 0.4, , 0.2, , ( i), , ( ii ), , (iii), , X, , 0, , 1, , 2, , 3, , 4, , P (X), , 0.1, , 0.5, , 0.2, , -0.1, , 0.2, , X, , 0, , 1, , 2, , P (X), , 0.1, , 0.6, , 0.3, , Y, , -1, , 0, , 1, , P (Y), , 0.6, , 0.1, , 0.2, , (iv), , 4. Find mean for the following probability distribution, X, , 0, , 1, , 2, , 3, , P(X=4), , 1, 6, , 1, 3, , 1, 3, , 1, 6, , 5. State whether the following is not the probability mass function of random, variable. Give reasons for your answer., X, , 3, , 2, , 1, , 0, , -1, , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 52 :
PHOENIX INSTITUTE OF MATHEMATICS, 0.3, , P(X=x), , 0.2, , 0.4, , 0, , 0.05, , III. Short Answers ( 2 marks ), , (1) Find the expected value and variance of r.v. X whose p.m.f. is given below., X, , 1, , 2, , 3, , P(𝑋=𝑥), , 1, 5, , 2, 5, , 2, 5, , (2) Find the probability distribution of number of heads in two tosses of a, coin ., (3) The probability distribution of X is as follows:, X, 0 1 2 3 4, P(𝑋=𝑥) 0·1 k 2k 2k k, , Find k and P [X < 2]., (4) The following probability distribution of r.v. X, X, , −3, , −2, , −1, , 0, , 1, , 2, , 3, , P(𝑋=𝑥), , 0.05, , 0.1, , 0.15, , 0.20, , 0.25, , 0.15, , 0.1, , Find the probability that (i) X is positive. (ii) X is odd, (5) In the p.m.f. of r.v. X, X, , 1, , 2, , 3, , 4, , 5, , P(𝑋=𝑥), , 1, 20, , 3, 20, , 𝑎, , 2𝑎, , 1, 20, , Find 𝑎 and obtain c.d.f. of X., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 53 :
PHOENIX INSTITUTE OF MATHEMATICS, IV. Short answers ( 3 Marks), (1) Find the probability distribution of the number of successes in tosses of a die,, where a success is defined as number greater than 4 appears on at least one die., (2) A coin is biased so that the head is 3 times as likely to occur as a tail. If the coin, is tossed twice, find the probability distribution of tails.., (3) A random variable X has the following probability distribution:, X, , 0, , 1, , 2, , 3, , 4, , 5, , P(X), , 0, , k, , 2k, , 2k, , 3k, , k2, , Determine :, , ( i) k, , ii)P(𝑋 < 3), , 6, , 7, , 2 k2 7k2+k, , iii)𝑃(𝑋 > 4), , (4) Find the probability distribution of the number of doublets in three, throws of a pair of dice., (5) Find the mean and variance of the number randomly selected from 1 to 15., 3−𝑥, , (6) Let the p.m.f. of r.v. X be 𝑓(𝑥) = { 10, , , for 𝑥 = −1, 0, 1, 2, 0, otherwise, , Calculate E(X ) and Var (X )., (7) Find the probability distribution of the number of successes in two tosses of a, die, where a success is defined as six appears on at least one die., V. Long answers ( 4 Marks), , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 54 :
PHOENIX INSTITUTE OF MATHEMATICS, 1.Let a pair of dice be thrown and the random variable X be the sum of the numbers, that appear on the two dice. Find the mean or expectation of X and variance of X., 2. Two cards are drawn simultaneously (or successively without replacement) from a, well shuffled of pack of 52 cards. Find the mean, variance and standard deviation, of the number of kings drawn., 3. Two numbers are selected at random (without replacement) from the first six, positive integers. Let X denote the larger of the two numbers obtained. Find E, (X)., 4. In a meeting,70% of the members favor and 30% oppose a certain proposal. A, member is selected at random and we take X=0 if he opposed, and X=1 if he is in, favor. Find E(X) and Var (X) ., 5. The following is the c.d.f. of r.v. 𝑋, X, , −3, , −2, , −1, , 0, , 1, , 2, , 3, , 4, , F(𝑥), , 0.1, , 0.3, , 0.5, , 0.65, , 0.75, , 0.85, , 0.9, , 1, , Find p.m.f. of X. (i) 𝑃 (– 1 ≤ 𝑋 ≤ 2) (ii) 𝑃 (𝑋 ≤ 3/ 𝑋 > 0)., 6. A player tosses two coins he wins Rs.10 if 2 heads appears , Rs. 5 if 1 head, appears and Rs.2 if no head appears. Find the expected winning amount and variance, of winning amount., 7.From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at, random with replacement. Find the probability distribution of the number of, defective bulbs., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 55 :
PHOENIX INSTITUTE OF MATHEMATICS, 8. Let X denote the sum of the number obtained when two fair dice are rolled. Find, the standard deviation of X., 8. BINOMIAL DISTRIBUTION, Q.1) Multiple Choice Questions ( M.C.Q), , 2m, , 1. In a Binomial distribution with n = 4, if 2 P( X=3) = 3 P (X =2), then value, of p is ................, a), , 9, 13, , b), , 4, 13, , c), , 6, 13, , d), , 7, 13, , 2. Given that X ~ B (n, P). If n = 10, P = 0.4 then E(X) = ..............., a) 1, , b) 2, , c) 3, , d) 4, , 3. For X ~ B (n, P), If v(x) = 2.4 and P = 0.4 then n = .............., a) 10, , b) 20, , c) 30, , d) 40, , 4. Given that X ~ B ( n = 10, P ), E (X)= 8 then value of P = ........, a) 0.4, , b) 0.8, , c) 0.6, , d) 0.7, , 5. Bernoulli distribution is a particular case of binomial distribution if n =, ..........., a) 4, , b) 10, , c) 2, , d)1, , II. Very Short Answers ( 1 mark ), i) If X ~ B(n,P) , E (X) = 12, V(X) = 4 then find n, ii) For Bernoulli Distribution , state formula for E(X) and V(X), iii) For X ~ B(n , P) and P(X=x) = 8Cx (1/2)x (1/2)3-x then state values of n and P, iv) State the formula for p.m.f of Binomial Distribution., v) A die is thrown . If X denotes the number of positive divisor of the outcomes, then find the range of random variable X., III. Short Answers ( 2 marks ), i) A r.v X ~ B( n,P) . If the value of mean and variance of X are 18 and 12, respectively then find total number of positive value of X., ii) Given X ~ B(n,P) , If E(X) = 6, V(X) = 4.2 find n and P, iii) If X ~ B( n, P) with n = 10 , P = 0.4 then find E (X2), iv) If X ~ B( 6, P) and 2. P( X =3) = P( X=2) then find P., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )

Page 56 :
PHOENIX INSTITUTE OF MATHEMATICS, 5, , 4, , v) Let the p.m.f of r.v.x be p(x) = 4Cx ( )x ( )4-x , x =0,1,2,4 Find E(X) and, 9, 9, Var (X), IV. Short answers ( 3 Marks), i) A Fair coin is tossed 5 times , find the probability that a) coin shows exactly, three times head b) no head., ii) The probability that certain kind of component will survive a cheak test is 0.6., Find the probability that exactly 2 of the next 4 tested components survive., iii) Find the probability of guessing correctly at least nine out of ten answers in, a "true" or "false" objective test., iv) A fair coin is tossed 8 times. Find the probability that it shows heads i), exactly 5 times ii) at least once., v) The Probability that a person who undergoes a kidney operation will be, recovered is 0.5. find the probability that out of 6 patients who undergo similar, operation a) none will recover b) half of them recover., , UNDER THE GUIDENCE OF MR.VINOD KAMBLE SIR (9860574777 / 9130777567 )