Page 1 :
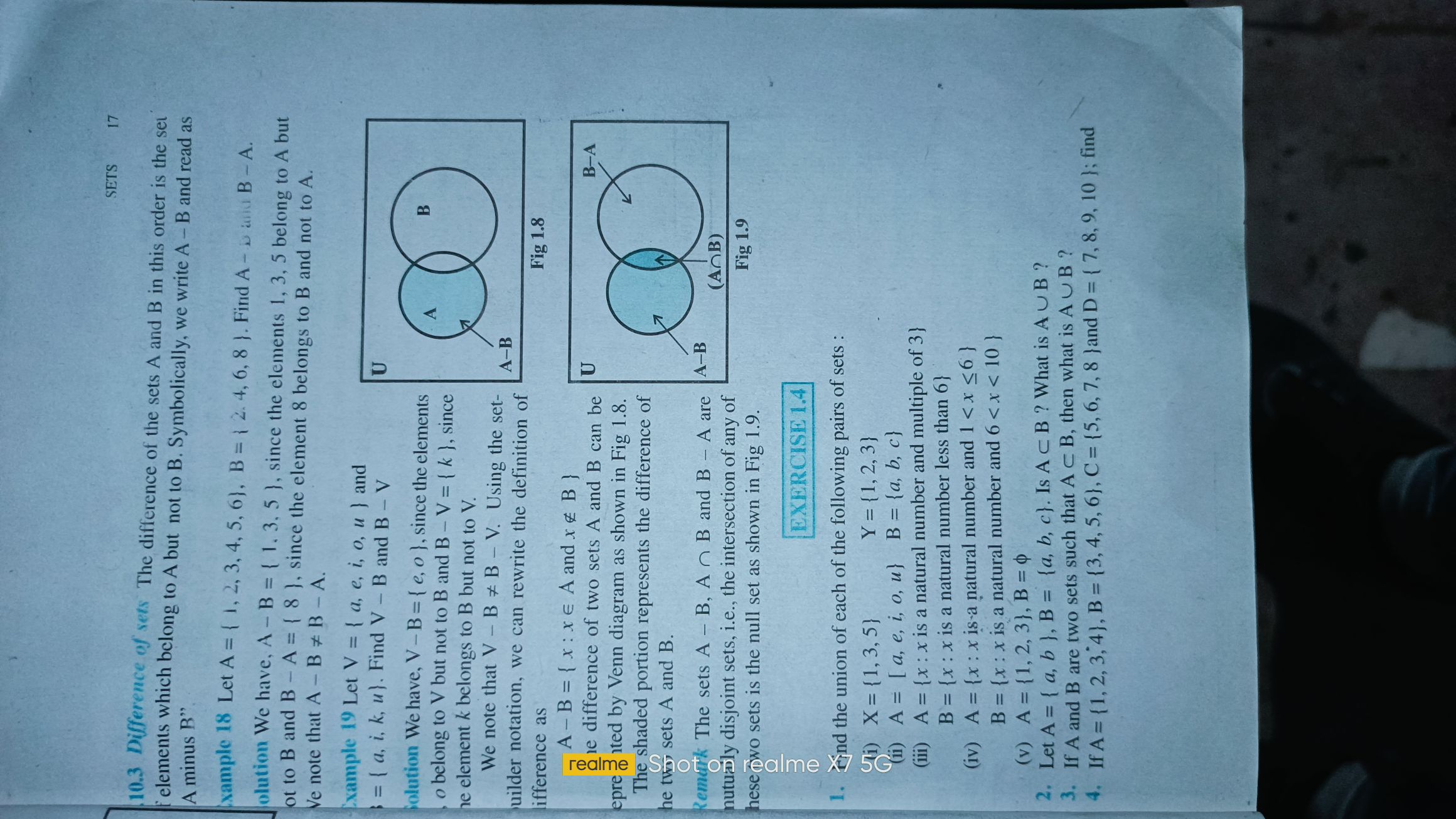
SETS 17, 10.3 Difference of sets The difference of the sets A andB in this order is the set, elements which belong to A but not to B. Symbolically, we write A- B and read as, A minus B",, xample 18 Let A = { 1, 2, 3, 4, 5, 6), B = 2. 4, 6, 8 }. Find A- and B- A., olution We have, A- B { 1. 3, 5 }, since the elements 1, 3, 5 belong to A but, ot to B and B- A = { 8 ), since the element 8 belongs to B and not to A., Ve note that A -B B-A., xample 19 Let V = { a, e, i, o, u ) and, 3= { a, i, k, u}. Find V- B and B - V, %3D, Solution We have, V-B={ e, o}, since the elements, o belong to V but not to B and B- V = {k}, since, he element k belongs to B but not to V., We note that V-B B- V. Using the set-, uilder notation, we can rewrite the definition of, lifference as, B., 1., %3D, А-В, Fig 1.8, A - B = { x : xe A and x e B }, e difference of two sets A and B can be, B-A, epre ited by Venn diagram as shown in Fig 1.8., The shaded portion represents the difference of, he tw sets A and B., Remerk The sets A - B, A n B and B, nutualy disjoint sets, i.e., the intersection of any of, hese wo sets is the null set as shown in Fig 1.9., A are, А-В, (AOB), Fig 1.9, EXERCISE 1.4, nd the union of each of the following pairs of sets :, Y = {1, 2, 3}, Ti) X= {1, 3, 5}, (1i) A = [a, e, i, o, u} B = {a, b, c}, (iii) A = {x:x is a natural number and multiple of 3}, B = {x: x is a natural number less than 6}, (iv) A = {x: x is a natural number and 1 <x <6 }, B = {x:x is a natural number and 6 <x < 10 }, (v) A = {1, 2, 3}, B = 0, 2. Let A = { a, b }, B = {a, b, c}. Is AcB ? What is AUB ?, 3. If A and B are two sets such that AcB, then what is AUB ?, 4. If A = {1, 2, 3,4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find