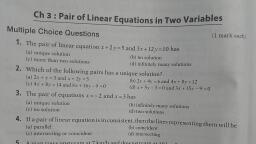Page 1 :
the ce ee n e, sapa e, wi a, ideos etc., - 12, Frm gh sgtest wng, Assertion-Reasoning Type MCQS, Direction: In the question no. 48 to 51 a statements, assertion (A) is followed by a statement of reason, 49. Assertion (A): Pair of linear equations:, 9x + 3y + 12 = 0, 8x + 6y + 24 = 0 have, infinitely many solutions., Reason (R): Pair of linear equations, (R). Mark the correct choice as, (a) Both Assertion (A) and Reason (R) are true, a;x+by+cj, =0 and ax+ b,y+c=0 have, and Reason (R) is the correct explanation, of Assertion (R)., infinitely many solutions, if, (b) Both Assertion (A) and Reason (R) are, the true but Reason (R) is not the correct, 50. Assertion (A): 3x – 4y= 7 and 6x – 8y =k, have infinite number of solution if k= 14., explanation of Assertion (A)., (c) Assertion (A) is true but Reason (R) is, Reason (R):a,x + b,y + c, = 0 and a,x +, false., by+c2, = 0 have infinitely many solutions, if 4 b,, az b2 C2, 51. Assertion (A): The linear equationsx-2y-3=D0, (d) Assertion (A) is false but Reason (R) is, true., 48. Assertion (A): If the system of equations, 2x + 3y = 7 and 2ax + (a + b)y = 28 has, and 3x + 4y – 20, 0 have many infinitely, one solution, then 2a - b = 0, solutions., Reason (R): The system of equations 3x-5%3D9, and 6x - 10y = 8 has infinitely many, Reason (R): The linear equations 2x+3y-93D0, and 4x + 6y – 18 = 0 have infinitely many, solution., solution., Case-Based MCQS, 1. General form of pair of linear equations in, two variables is a,x+by+c,%3D0anda,x+ by, =0. If graph of pairs of linear equations, (i) parallel, (ii) intersecting at(2, 2), (iii) coincident, (iv) intersecting at (5, 5), to, = 0 and a,x + b,y + c, 0., 4,x + b,y +, represent two intersecting lines then point of, intersection is the solution of pair of linear, equations. If graph represent two parallel, lines then pair of linear equations has no, common solutions. If graph represents, two coincident lines then pair of linear, equations has infinitely many solutions., Answer the questions based on above., (a) The pair of equations x, y = 5 graphically represents lines, which are, %3D, (b) For the linear equation 2r+ 5y-8=Q,, the another linear equation in two, variables such that the graphical, representation of the pair so formed, represents parallel lines is, (i) 4x + 10y - 20 = 0, (ii) 14x + 20y – 20 = 0, 5 and, (iii) 16x + 15y – 20 = 0, %3D, (iv) 2x – 5y – 20 = 0