Page 1 :
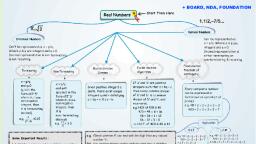
UNIT I: ALGEBRA, , QUADRATIC, EQUATIONS, , , , , , , , , , , Syllabus, , Standard form of a quadratic equation: ax’ + bx + c= 0, where (a # 0). Solutions of quadratic equations (only, real roots) by factorization and by using quadratic formula. Relationship between discriminant and nature of, roots., , Situational problems based on quadratic equations related to day to day activities (problems on equations, reducible to quadratic equations are excluded)., , , , , , (@) Learning Outcomes, , » Students will be able to identify the quadratic equation in standard form., > Students can find the roots quadratic equation., , » Students will be able to understand the nature of roots., , » Students can apply the concept of quadratic equation in real life problems., , , , , , , , , , i=) Revision Notes, , Sol, , , , ns of Quadratic Equations, , > A quadratic equation in variable x is of the form ax” + by + c = 0, where a,b and c are real numbers and a 0., , > The values of x that satisfy the equation are called the solutions or roots or zeros of the equation., > Areal number ozs said to be a solution/root or zero of the quadratic equation ax? + bx + ¢ = 0, ifac? + ba + c= 0., » A quadratic equation can be solved by the following algebraic methods:, (i) By factorization (splitting the middle term),, (ii), Making perfect squares and, (iii) Using quadratic formula., > Ifax? + bx +c = 0, where a #0 can be reduced to the product of two linear factors, then the, roots of the quadratic equation ax* + bx + c = 0 can be found by equating each factor to zero., > Method for factorization of the equation ax? + bx + ¢ = 0, where a #0., (i) Find the product of a and c ie, “ac”

Page 3 :
(ii) Find a pair of numbers b, and b, whose product is “ae”and whose sum is “b” (if you can’t, find such number, it can’t be factorized), (iii) Split the middle term using b, and b,, that expresses the term by as bjx + b,x. Now, factorize, by grouping the pairs of terms., » Roots of the quadratic equation can be found by equating each linear factor to zero. Since,, product of two numbers is zero, then either or both of them are zero., > Solution of a Quadratic equation using Quadratic formula, The roots of the quadratic ax? + by + c = 0; a #0 can be find using the following formula:, ee b+ Vb? —4ac, 2a, The above result is known as quadratic formula or Sridharacharya Formula., Here, l? - 4ac > 0, for real roots., » The Old-Babylonians (400 BC) stated and solved problems involving quadratic equations., » The Greek mathematician Euclid developed a geometrical approach for finding out roots, which are solutions of, quadratic equations., > Brahmagupta (C.E. 598-665) gave an explicit formula to solve a quadratic equation of the form ax* + bx +c = 0., » Sridharacharya (C.E. 1025) derived the quadratic formula for solving a quadratic equation by the method of, completing the perfect square., » An Arab mathematician Al-Khwarizmi (about C.E. 800) studied quadratic equations of different types., » Abraham bar Hiyya Ha-nasi, in his book ‘Liber Embadorum’ published in Europe in C.E. 1145 gave complete, solutions of different quadratic equations., , Discriminant and Nature of Roots, , > For the quadratic equation ax* + by + c = 0, the expression /* — dac is known as discriminant, ie., Discriminant D = lP — 4ac., , » Nature of roots of a quadratic equation:, (i) If —4ac > 0, the quadratic equation has two distinct real roots., (ii) If — dac = 0, the quadratic equation has two equal real roots., (iii) If — dac < 0, the quadratic equation has no real roots., , % Mnemonics, , , , , , 2, Concept: To Find the roots of quadratic equation, — 2 —4ac |, a, , A Negative Boy could not decided if he did or didn’t want to go to a Radical party. The Boy, was Square so he missed out on 4 Awesome Chicks., , This was all over by 2 a.m., Interpretation:, A negative Boy = (-b), he did or didn't want to go = (+/-), , , , To a Radical party = ), , Boy was Square = (b?), Missed out = (-), 4 Awesome = 4a, Chicks =¢, All over = Divided by, 2a.m. =2a

Page 5 :
(a) Vast Ext t=0, , (D) 3x7-3x+3=0 U, Ans. Option (B) is correct., , , , Explanation: -x° + 3x On comparing with ax” +bx +c = 0, , , , a=-1b=3,c=-3, , = Sum of the roots = og, a, , =1, 6. The roots of the equation x7 + 7x + 10 = O are:, (A) -5,-2 (B) 5,2, (C) 5,-2 (D) -5,2, , Uj [CBSE SQP 2020-21], Ans. Option (A) is correct., Explanation: Given, x + 7x + 10 = 0, , Comparing with ax° + bx + c = 0, we get, a=1,b=7andc=10, , —b+ Vb? —4ac, , 2a, , ~7+ (7) -4«1x10, , , , , , , , , , , , >, “3 en EH, 2, P48 SHED, > or, 2 2, > x=-2 or-5, , Hence, the roots of the given equation are — 2, and -5., 7. Which of the following equations has two distinct, real roots?, , (A) ax? -3V2n+2=0 (B) 2 +x-5=0, , (C) x74+3x+2V2=0 (D)5x7-3r+1=0 U, Ans. Option (B) is correct., , Explanation: et+x-5=0, On comparing with ax? +bx +c = 0, a=1,b=1,c=-5, — dac = (1)? 4 (1) (-5), = 14+20, = 21>0, Since D (ie., ? - 4ac) > 0, Hence, the equation has two distinct real roots., 8. Values of & for which the quadratic equation, 2x? ky + k = 0 has equal roots, is:, (A) 0only (B) 4, (C) 8 only (D) 0,8 Ri, Ans. Option (D) is correct., , Explanation: Given equation is 2x7 - kx + k = 0, On comparing with ax? + bx +c =0, @=2,b=-ke=k, For equal roots b?, Ck? -4 2K), R-8k, , , , k(k-8), k=0,8, Hence, the required values of kare 0 and 8., 9. The quadratic equation 2x7 — /5x + 1=0 has, (A) two distinct real roots, (B) two equal real roots, (C) no real root, (D) more than 2 real roots U, , Ans. Option (C) is correct., , Explanation: 2x7 — 5x +1=0, , On comparing with ax? +bx +c = 0, a=2,b= -V5,c=1, , Discriminant = b? - dac = (—V5 )* - 4(2)(1), , =5-8=-3<0, Since D (i.e., b” - 4ac) < 0, Therefore, the equation has no real root., , 10. Which of the following equations has no real root?, (A) x7 -4x+3V2=0 (B) x7 +4x-3V2 =0, , (QC) x7 -4x-3V2=0 (D) 3x7 +4V3x+4=0 U, Ans. Option (A) is correct., , , , Explanation: x° -4x+ 3v2 =0, On comparing with ax +bx +c =0, , a=1,b=-4,c=3V2, Discriminant = b? - 4ac, , = 4)F-4()v2), , 16-122, 16-12 x 1.41, 16 - 16.92, =-092<0, Since, D<0O, Therefore, the equation has no real roots., , nw, , 11. (7 + 17-27 = Ohas, (A) four real roots, (C) no real roots, Ans. Option (C) is correct., , (B) two real roots, (D) one real root. uU, , , , Explanation: (3° + 1), xt41427-7, weet, , , , Let, , , , y+y+1=0, On comparing with ay” +by +c = 0, a=1,b=1,c=1, Discriminant, D = b* = 4ac, , (1)? -4(1)q), 1-4, , , , Since, Therefore, the equation has no real roots.