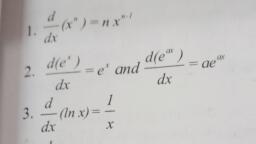Page 1 :
1. Choose the correct option., i) The resultant of two forces 10 N and 15 N, ‘acting along +x and - x-axes respectively,, is, , iv), , , , (B) 25 N along - x-axi, , (C) 5 Nalong + x-axis, , (D) 5 N along - x-axis,, , For two vectors to be equal, they should, , have the, , (A) same magnitude, , (B) same direction, , (C) same magnitude and direction, , (D) same magnitude but opposite direction, , iii) The magnitude of scalar product of two, unit vectors perpendicular to each other is, (A) zero (B)1, (©)-1 (D)2, , iv) The magnitude of vector product of two, unit vectors making an angle of 60° with, cach other is, t (B)2, (32 (D) 3/2, , v) If A,B and © are three vectors, then, which of the following is not correct?, , vy), , iii), , , , (0) Fx(B4T)=xBs BT, 2. Answer the following questions., , Show that 4 a unit vector,, , , , If V,=3i+4j+kandv, =i-j-k,, determine the magnitude of ¥i+ V3, , [Ans: 5], For vj=2i-37 and ¥,=-6i+57,, determine the magnitude and direction of, vtw., , [am 2V5, 0 = tan" (-3} with sa], , , , vi), , , , iii), vii), , Find a vector which is parallel to V., and has a magnitude 10, i, , [ans:, , , , , , i, v5 V5, , , , Show that vectors 3=2i+57-6k and, Sx, , 3k are parallel., , , , 3. Solve the following problems., , +37 and, , , , teicnine sige 2, , b= 31457 [Ans:é], , Show that vectors g=2)+37+6k,, b=31-6]+2k and ¢=6)+2)-3k are, mutually perpendicular,, Determine the vector product of, Vj =2i+3j-kand v, =i+2)-3k,, , [ans Ti+ 5] +k], , , , , , , , Given ¥,=5i+2} and ¥,=0i-6) are, perpendicular to each other, determine the, , value of a., weae 2, 5, , Obtain derivatives of the following, functions:, , , , , , , , (i)xsinx (ii) x*+cos x, (iii) xinx, ‘Ans :(i)sin x +x.c0s x,, (ii) 4° -sin x, (iii) meee, sinx sin?x, , Using the rule for differentiation for, quotient of two functions, prove that, , d (sinx ;, =| = |=scc’x, dx \ cos x, , Evaluate the following integral:, Gf sinxde Gi) [xd, [Ans : (i) 1,(ii) 12], , “se